1 – Mach et vitesse du son dans un milieu :

          A. Les vitesse subsoniques, transsoniques et supersoniques :

                      •  On dit qu'un avion vole à vitesse subsonique lorsque sa vitesse est très inférieure à celle du son, c'est à dire inférieure à 300 m/s.

                      •  On dit qu'un avion vole à vitesse transsonique (ou sonique) lorsque sa vitesse est comprise entre 300 m/s et 380 m/s, ce qui correspond à un nombre de Mach proche de 1.

                      •  On dit qu'un avion vole à vitesse supersonique lorsque sa vitesse dépasse les 380 m/s, ce qui correspond à un nombre supérieur au nombre de Mach critique supérieur.

                      •  Au-dessus de Mach 5, c'est-à-dire environ 1,7 km/s, la vitesse est dite hypersonique, très peu d'avions conventionnels atteignent ces vitesses (ex : le X-43).

          B. La vitesse du son dans l'air :

          La vitesse du son dans l'air se mesure en Mach, en l'honneur du physicien autrichien Ernst Mach qui, vers 1880, mit pour la première fois en évidence le rôle de la vitesse du son aérodynamique. Le nombre de Mach M est défini par la relation :     

                                                   où a est la vitesse de l'objet et c la vitesse locale du son ;

     vitesse locale, car Ernst Mach avait découvert que la vitesse du son variait en fonction de la température de l'air. Dans les modèles couramment utilisés en aéronautique, on utilise une atmosphère standard. De plus, la vitesse du son est fonction de la température selon la formule :

Dans le cas particulier de l'air où             , M = 29.10 - 3 kg .mol -1, et R = 8,314 J.K.mol -1 , on a :

(T la température en Kelvin : T = t° - 273,15)

          On obtient donc le graphe suivant (on notera l'aspect quasi-linéaire de cette fonction pour les altitudes comprises entre 0 et 11.000 mètres ) :

          C'est également Ernst Mach qui mit en évidence les phénomènes d'onde de choc, qu'il étudia dans le cas de projectiles et de gaz à haute pression. Une onde de choc correspond à une brusque variation des paramètres physiques tels que la densité, la température, et surtout, la pression sur le front de la perturbation.

     2 – Le cône de Mach

          Si on considère un avion suivant une trajectoire rectiligne, sa vitesse est constante et supérieure à celle du son. La succession des ondes sonores émises tout au long de son déplacement produit un cône de choc supersonique, comme illustré sur les schémas suivants. Dans cet exemple, la vitesse de l'avion est égale à 1,5 fois la vitesse du son.

Le cône de choc est matérialisé par la tangente aux différents cercles correspondants à la propagation des ondes sonores, sur les schémas, seuls trois cercles ont été représentés. Chaque cercle correspond à l'onde sonore émise alors que l'avion se trouvait au point de même couleur que le cercle.

Le demi-angle au sommet du cône de choc n'est pas quelconque, il est lié à la vitesse de propagation du son et à la vitesse de l'avion.

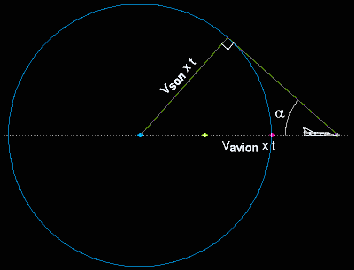
Pendant la durée t, l'avion a parcouru la distance :

L'onde sonore a "parcouru" la distance :

La relation trigonométrique dans le triangle rectangle représenté ci-dessous donne :

Si la vitesse de l'avion est égale à celle du son, le demi-angle au sommet Alpha est égal à 90 °. Plus la vitesse sera élevée, plus l'angle Alpha sera aigu.

          Cette relation peut être utilisée pour déterminer la vitesse d'un objet supersonique dès lors que le cône de choc est matérialisé d'une façon ou d'une autre.

          B. Utilisation de l'angle du cône de choc pour déterminer la vitesse d'un avion

          Il est très simple d'utiliser la relation précédente pour déterminer la vitesse d'un avion supersonique lorsque le cône de choc est visible. Pour appliquer cette méthode au F-4 Phantom ci-dessus, il suffit de matérialiser les deux droites limitant le cône de choc et de mesurer l'angle qu'elles forment. Pour des raisons de précision évidente, on mesurera l'angle 2xAlpha et non pas l'angle Alpha.

Sur cet exemple, l'angle 2 x Alpha est égal à 120°, donc Alpha = 60°. Le rapport des vitesses est donc :

                soit

     L'avion vole donc à la vitesse de Mach 1,15, c'est à dire (avec la vitesse du son supposée égale à 340 m/s) : 391 m/s ou 1407 km/h.

          Il est très inhabituel qu'un avion ( fût-il un avion militaire ) vole si bas à une telle vitesse, l'explication est simple, il s'agissait d'un prototype utilisant un radar de suivi de terrain permettant au pilote de fixer exactement l'altitude à laquelle l'avion devait se maintenir sans risque d'accident. De tels dispositifs équipent nombre d'appareils modernes comme les Mirages 2000, les Tornado européens ou les Sukhoi Su-24 russes....